Ksp

\begin{equation} \begin{split} {E}_{cell} & = {E}^{\circ }-\frac{RT}{nF}\times ln(Q) \\ ln(Q) & = ({E}_{cell} - {E}^{\circ })\times \left(-\frac{nF}{RT}\right) \\ &=\frac{x\ moles\ {PbCl}_{2}}{0.693\ moles\ {{Pb(NO}_{3})}^{2}} \\ \\ &; where\ Q= the\ reaction\ quotient \\ &;and\ {E}_{cell}=the\ voltage\ across\ the\ lead\ plate \\ &;and\ R = molar\ gas\ constant,\ \approx 8.314\ Joules/mole\ K \\ &;and\ F=Faraday\ constant,\ \approx 96,485 \\ &;\ \ \ \ \ \ \ \ \ \ \ \ (\sim 9.65\times {10}^{4})\ Coulombs/mole\ K \\ \end{split} \end{equation}
Example Problem

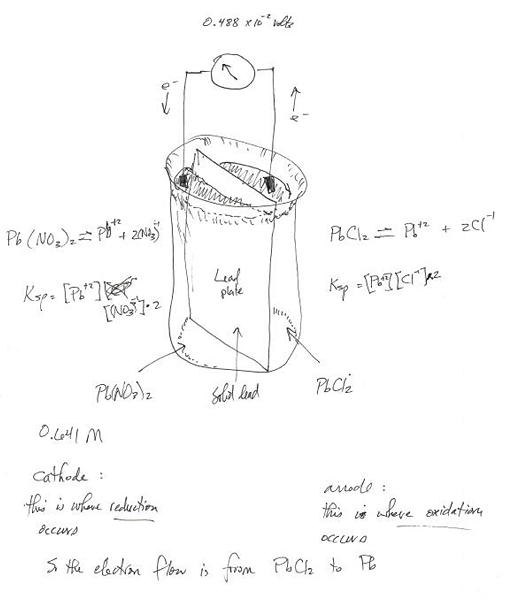
A student does an experiment to determine the molar solubility of lead(II) chloride. He constructs a voltaic cell at 298 K consisting of 0.693 M lead nitrate solution and a lead electrode in the cathode department, and a saturated lead chloride solution and a lead electrode in the anode compartment.
If the cell potential is measure to be 4.96 X 10^-2 V, what is the value of {K}_{sp} for lead chloride at 298 K based on this experiment?

Once again, here are the givens.
\begin{equation} \begin{split} {E}_{cell} & = 0.0496\ or\ {4.96}^{-2}\ Volts \\ n & = 2\ moles\ of\ electrons\ transferred \\ & \ \ \ \ \{i.e.,\ {Pb}^{\circ }+2{Cl}^{\circ }\rightleftharpoons {PbCl}_{2}+2{e}^{-}\} \\ {E}^{\circ }&=0.0000\ Volts \\ & \ \ \ \ \{the\ voltage\ at\ steady\ state\ equilibrium\} \\ T & =298\ K \\ & \ \ \ \ \{temperature\ in\ Kelvin\ degrees\} \end{split} \end{equation}
Calculating the Result
\begin{equation} \begin{split} 0.0496\ V & = 0.0000\ V -\frac{8.314\ Joules/mol\ K\times 298\ K}{2\ moles\ {e}^{-}\times 96,485\ Coulombs/mole}\times ln\left(\frac{\ M\ moles\ {PbCl}_{2}}{0.693\ moles\ {{Pb(NO}_{3})}^{2}}\right) \\ ln\ \left(\frac{x\ M}{0.693}\right)&=(0.0496-0.0000)\times\left(- \frac{2\times 96,500}{8.314\times 298}\right) \\ ln\ \left(\frac{x\ M}{0.693}\right)&=\ \sim -3.864 \\ x\ M&=\ \sim 0.693\times {e}^{-3.864} \\ &=\ \sim 0.693\times 2.10\times {10}^{-2} \\ x\ M&=\ \sim 1.46\times {10}^{-2}\ molar\ solubility\ of\ {PbCl}_{2} \\ \end{split} \end{equation}
Ksp Calculation for a Saturated Lead Chloride Solution
In the equation.
\begin{equation} \begin{split} {PbCl}_{2}&\rightleftharpoons {Pb}^{-2}+2{Cl}^{-1} \\ [{PbCl}_{2}]&=x\ M \\ [{Pb}^{2+}]&=x\ M \\ [{Cl}^{-}]&=2x\ M \\ \\ \end{split} \end{equation}
So plugging this all in for the solubility product
\begin{equation} \begin{split} {K}_{sp}&=[{Pb}^{2+}]\times {[{Cl}^{-}]}^{2} \\ &=(x)\times {(2x)}^{2} \\ &=x\times 4\times {x}^{2} \\ &=4\times {x}^{3} \\ &=4\times {(1.46\times {10}^{-2})}^{3} \\ {K}_{sp}&=\ \sim 1.2\times {10}^{-5} \\ \end{split} \end{equation}